Quantum Operators: What are they?

 Quantum Operators: What are they?

Frank Lin

If you've been learning a bit about the actual physics behind quantum physics, you've likely come across these things called operators. When I was first starting out in quantum mechanics, I was perplexed by the abstractness of them. All explanations of what an "operator" really was just didn't make sense to me, and those explanations often contradicted themselves. I think it is fair to say that operators are generally not explained well--even by textbooks and professionals. The goal of this blogpost is to make you understand what a quantum operator really is.

An Operator is something that acts on an eigenfunction and outputs the associated eigenvalue multiplied by the same eigenfunction.

What a mouthful! Let's break this statement into parts. We have 3 complex words: Eigenfunction, eigenvalue, and operator. To know what an operator is we need to know what an eigenfunction and eigenvalue is. To know what those are, let's review some basic linear algebra.

From Linear Algebra, we know that matrices act on vectors and output new vectors, just like how functions act on scalars and return new scalars. Here's an example. 

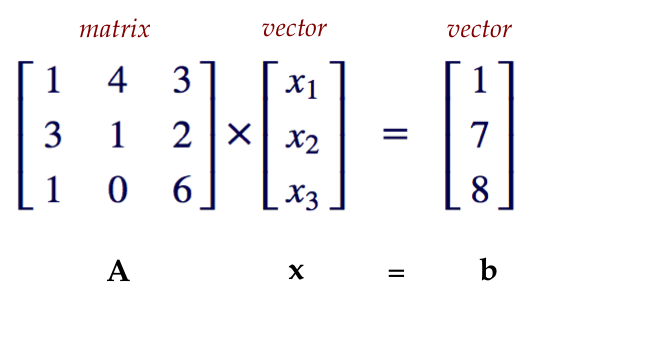
A is a matrix. A acts on vector x and outputs another vector b. What does this mean visually though?

It means that the matrix is acting on one vector and scaling + rotating it by some amount to form a new vector. Matrixes are just linear transformations (also called linear maps)! Focus on just one colored arrow on the above image. Here, the matrix T acts on vector #2 and scales + rotates it by some amount to form a new vector. Now focus on both sets of vectors. The same matrix acts on different vectors and treats them differently. It rotates vector #1 a lot but does not scale it by much. But when the same matrix acts on vector #2, it rotates it only a little, but scales it by a lot (it's length completely changes!). I hope you now see that when a matrix acts on a set of vectors, it will treat each initial vector differently. 

Footnote**: You can even find out how much the vector has been scaled + rotated after being acted upon by a matrix. To find how much it has been scaled, find whether or not the new vector lies in the span of the first, and find the exact multiple needed (in other words, if M(v)=w, then solve for a (w=av).  To find how much it has been rotated, you'd need to use the metric tensor.

This linear algebra review probably looks nothing like our original question, but it relates very much. Let's now directly answer the question on what an eigenvector is. An eigenvector is a vector that when acted upon by a matrix is only scaled by a particular amount. The amount that it has been scaled is the eigenvalue. Let's put this in math language.

If M(v)=av, then v is the eigenvector and a is the eigenvalue. 

As we can see from the above image, vector x has only been scaled by some amount when acted by matrix A. It has not been rotated at all. This means that vector x is the eigenvector of matrix A, and lambda is the eigenvalue of vector x. Hopefully that has been nailed into your head enough. Now something looks very interesting here. Let's go back to our original definition...

"An Operator is something that acts on an eigenfunction and outputs the associated eigenvalue multiplied by the same eigenfunction"

And our second definition 

"An eigenvector is a vector that when acted upon by a matrix is only scaled by a particular amount. The amount that it has been scaled is the eigenvalue"

The similarity of these two definitions is no coincidence. An eigenfunction is just an eigenvector, but for functions. And what acts on eigenvectors? Matrices! This means that an operator is just a linear map that acts on a function and returns some scalar value multiplied by that very same function if that function is an eigenfunction. Let's finally tie all of this in the context of quantum mechanics.

The Q operator acts on an eigenfunction A and returns the same eigenfunction A multiplied by an eigenvalue q, where q represents an observable quantity. Let's give specific examples. The position operator acts on the wave function, and spits out the same wave function multiplied by the position eigenvalue. The position eigenvalue represents the definite position of a particle. The momentum operator acts on the wave function and spits out the same wave function multiplied by the definite momentum of the particle. 

The Energy operator (also called the hamiltonian) acts on the wave function and returns the same wave function multiplied by the definite energy of the particle the wave function describes. Hopefully you see the pattern here. Now it is good to note that not all wave functions satisfy the "eigenvalue problem" which is what these kinds of equations are called. The only wave functions that satisfy these equations (except for the hamiltonian one) are called eigenfunction wave functions. This reasoning may seem circular because it is. The eigenvalue problem only works for eigenfunctions, and the definition of an eigenfunction is a function that works in the eigenvalue problem. Put shortly, the eigenvalue problem equation works when it works, and when it does work, that function is an eigenfunction. It also turns out that no realistic particles could ever be described by eigenfunctions (except for hamiltonian), since you would know the definite momentum, position, etc., of a particle which violates the Heisenberg uncertainty principle (see my last post about that one). 

You may now have the impression that eigenfunctions are useless, since they do not describe real states. Hope is not lost though, because a superposition of eigenfunctions can actually describe real states. Take the free particle potential for example. The wave function for a free particle is e^(-ikx+vt) where k is the quantum state and v is the velocity of the wave. e^(-ikx+vt) is a plane wave equation, and when you multiply it by the momentum operator, you actually get a real constant multiplied by the same wave function (that constant being hk). Since the wave function for single free particle states are eigenfunctions, they cannot describe real particles. However, a superposition of all possible states can yield a non-eigenfunction where the uncertainty principle holds. We won't be diving into the math of that, but it is a good example because it shows how superpositions of non-real states can yield real states, and that's just cool.

Here's a table of various operators in quantum mechanics

When you multiply all of these by an eigenfunction, you get the associated observables as the eigenvalues, and that's about it. Now if you've been paying close attention, you may have noticed that the famous Schrodinger Equation is literally just an eigenvalue problem. 

We'll be delving more into this equation in the near future. It's amazing how properties of linear algebra transfer so well to quantum physics.